Research

Byzantine-Resilient Distributed Computing

Undergraduate thesis with Prof. Nikhil Karamchandani and Prof. Vinod Prabhakaran.

We study a distributed computing scenario where the goal is to compute multiple possibly independent sub-tasks by distributing their computation among workers, some of whom may be malicious. Our work builds upon the setting introduced in this paper. We propose a protocol that successfully solves for all sub-tasks using an optimal number of local computations under no communication constraints, while characterizing the tradeoff between computation and redundancy. We also propose modifications to the protocol to improve communication performance without compromising on computation.

Our paper titled “Byzantine-Resilient Distributed Computation via Task Replication and Local Computations” was presented at the Information Theory Workshop (ITW) 2025.

Information-Theoretic Persuasion

Research project with Prof. Michael Gastpar.

We are studying a project that models persuasion using information theory. Consider an agent that attempts to persuade a worker into taking an action favorable to the former’s objective. The agent achieves this “persuasion” by revealing partial information about the worker’s objective.

We are currently working on quantifying this persuasion using the information contained in associated quantities and making remarks on the agent’s optimal choice of selective information revelation.

Our paper titled “The Persuasion Bottleneck” was presented at the International Symposium on Information Theory (ISIT) 2024.

Correlated Multi-Secret Sharing

Research project with Prof. Vinod Prabhakaran.

Multi-Secret Sharing is a problem in information-theoretic cryptography, that is similar in setting to the multi-party computation problem. It involves distributing a set of shares, such that each party learns their secret using the shares accessible to them, without learning any extra information about the secrets of the other parties.

I worked on the analysis of 3-party multi-secret sharing schemes under specific scenarios of the problem. I looked for optimal schemes and tested the optimality by bounding the randomness complexity required to facilitate secret sharing. We extended these information-theoretic bounds to all possible combinations of binary secrets and presented combinatorial bounds in cases where the lower bound was loose.

Our paper titled “Randomness Requirements for Three-Secret Sharing” was presented at the International Symposium on Information Theory (ISIT) 2023.

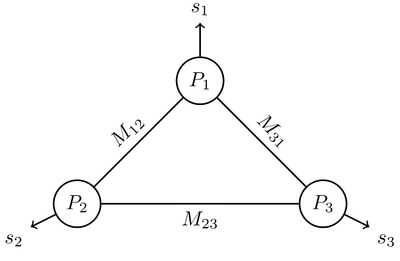
A general multi-secret sharing setting